Aly_

题意简述

• $n$ 点 $m$ 边无向图。 $n,m$ 未知，图的形态未知。你初始在某个点上，带了一个路标，目的是求出 $n,m$。
• 你可以：查看当前点的状况（相邻点数和是否有路标）；在一个点上拿起/放下路标；走到一个相邻节点。
• 特别注意的是：通过一条边走到相邻节点时，边的编号是临时确定的。即：把进入这个点时经过的边设为 $0$ 号，逆时针依次确定每一条边的编号。
• $n<=100,m<=4000$。

分析

​ 思维难度较高的题。

​ 容易想到一种......

​ 。

​ 。

​ 。

​ 然后发现什么方法都想不到。

​ 从最简单的地方开始考虑：我们肯定需要遍历这张图，这样才能确定 $n$。如果在遍历每个点时都记下与它相连的边数，我们还能确定 $m$。遍历图的方式，常见的有 DFS 和 BFS 。因为我们不知道这张图长什么样，所以采用 DFS 可能会带来一些优势。DFS 树上只有树边和返祖边。

​ 然后马上出现了一坨问题：如何确定当前点是以前没遍历到的？如何确定每条边的相对位置？如何确定每个点在其父亲的儿子中的位置？

​ 确定边的相对位置： 假设我们现在走到了 $i$ ，正准备继续从它开始遍历。我们记 $Ar_i$ 表示点 $i$ 把它父结点在它的邻结点中编号为 $0$ 时，它当前的子结点的编号是多少。每次处理完一个子节点并回溯到 $i$ 准备前往下一个点时，修改 $Ar_i$ 的值。如果要倒着走，就是 $d-Ar_i$（$d$ 是 $i$ 的邻边数）。

​ 这样，我们也可以确定当前子节点在父亲的相对位置了。

​ **确定新点：**假设我们现在走到 $i$ 的某个邻点 $j$ ，想确定 $j$ 是 $i$ 的祖先还是一个新的点。我们先把路标放在 $j$ 上，然后走到 $i$ 并不断跳父亲。最后如果跳到根了都没看到路标就说明这是一个新点，回到 $j$ 记录之并继续遍历，否则说明 $j$ 是 $i$ 的祖先，我们取走路标再返回 $i$ 。

​ 还有一种情况，就是 $j$ 可能是 $i$ 的非儿子的后代：如果情况是这样，我们肯定以前遍历过 $j$ ，也一定通过 $j$ 走到过 $i$ 。于是可以记 $fl_{i,j}$ 表示点 $i$ 把它父结点在它的邻结点中编号为 $0$ 时，编号为 $j$ 的结点是否遍历过了。在通过 $j$ 发现 $<i,j>$ 返祖边时，我们修改 $fl_i$ ：把路标放在 $j$ ，回到 $i$ ，依次看 $i$ 的每个邻点上是否有路标，找到了之后就取回路标，修改 $fl$ 并返回 $j$ 。在回到 $i$ 时如果发现当前边 $fl$ 为 $1$ 就跳过之。

​ 为帮助理解过程，手玩一下样例的前半部分：

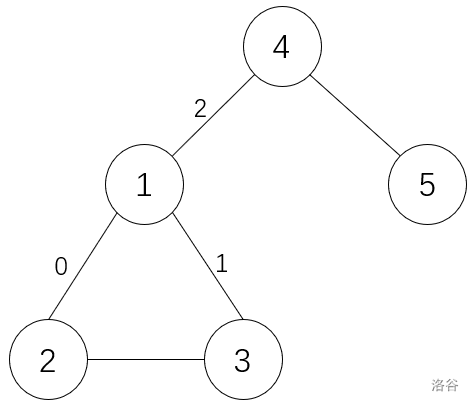
​ 我们初始在 $1$ 。走到 $2$ 并放下路标，回到 $1$ 发现没遇到路标，于是记录 $2$ 这个新点。回到 $2$ 拿起路标走到 $3$ ，放下路标，一路走回到 $1$ 都没看到路标，于是记录 $3$ 这个新点。回到 $3$ 拿起路标走到 $1$ 并放下，往回走并发现了路标，说明 $1$ 是 $3$ 的祖先。现在确定 $3$ 在$1$ 的相对位置，从树上走到 $3$ 放路标，走回到 $1$ ，在它的邻点转一圈之后发现 $1$ 号边通向了有路标的点。于是记 $fl_{1,1}=1$。回到 $3$ ，发现走完了，回到 $2$ ，发现也走完了，回到 $1$ 。$1$ 的下一条边的 $fl$ 为 $1$ ，跳过，走再下一条边，到 $4......$

​ 于是我们花了这么长的时间，终于把前三个点做出来了。考虑这样做的复杂度，无非是走每个点的时候都要回到根再回去。所以可能大概也许是 $O(n^2+nm)$ 的。标程实现较劣，很多实现方法都能过。

​ 据说我码风奇异：

void init();
void look(int&, bool&);
void put_sign();
void take_sign();
void walk(int);
void report(int, int);
#include<bits/stdc++.h>
using namespace std;
int d,n,m;
int ar[1001],fl[1001][1001],fa[1001],ns[1001];
bool si;
void dfs(int x){
	look(d,si);bool nfl=1;
	for(int i=(x!=1);i<d;i++,look(d,si)){
		if(fl[x][i]){
			if(!nfl)walk(1),walk(0);
			continue;
		}
		ar[x]=i;
		if(nfl)walk(i);
		else walk(1);
		put_sign(),walk(0),m++;
		int ni=x;
		while(!si&&ni!=1)walk(d-ar[ni]),ni=fa[ni],look(d,si);
		if(!si){
			fa[++n]=x,ns[x]=n;
			while(ns[ni])walk((ni==1)?0:ar[ni]),ni=ns[ni];
			take_sign(),dfs(n),nfl=0;
		}else{
			take_sign();int ng=ni;
			while(ni!=x)walk((ni==ng)?0:ar[ni]),ni=ns[ni];
			int nd=0,nj=0,tmp=0;
			put_sign(),walk(0),ni=fa[ni],look(d,si);
			while(ni!=ng)walk(d-ar[ni]),ni=fa[ni],look(d,si);
			bool nsi=0;
			look(nd,nsi);
			for(nj=1;nj<=nd;nj++){
				walk(1),look(tmp,nsi);
				if(nsi)take_sign();
				walk(0);
				if(nsi)break;
			}
			fl[ni][(ar[ni]+nj)%nd]=1,walk(nd-nj),ni=ns[ni],nfl=1;
			while(ni!=x)walk(ar[ni]),ni=ns[ni];
		}
	}
	look(d,si),walk(!nfl),ns[x]=ar[x]=0;
}
int main(){
	init();
	n++;
	dfs(1);
	report(n,m);
	return 0;
}

​ 没错，这题其实只是图上DFS