Aly_

题意简述

• 数轴上有 $n$ 个点，每个点有其位置 $x_i$ 和颜色 $t_i$，且在时间段 $[a_i,b_i]$ 中出现。总共有 $K$ 种颜色。
• 有 $q$ 个询问，每次询问在 $y_i$ 时刻所有颜色中距离位置 $l_i$ 最远的颜色。某个时刻下位置 $l_i$ 和颜色 $c_j$ 的距离定义为当时存在的所有颜色为 $ c_j$ 的点与 $l_i$ 距离的最小值。
• $n,q,K\le3\times10^5;x_i,t_i,a_i,b_i,l_i,y_i\le10^8$。

分析

​ 离散化+线段树二分。

​ 首先，询问和操作是离线的。容易想到把所有事件（点的出现，点的消失，询问）按时间排序后从小往大处理。

​ 先不考虑 $x_i$ 的范围，就假设所有的位置组成一个排列好了。

​ “最小值”的“最大值”，想到二分答案。

​ 顺着这个思路想下去，容易想到：每次询问时二分答案，假设当前二分的答案为 $X$，如果所有颜色都有至少一个点出现在了区间 $[l_i-X,l_i+X]$ 中，则说明所有颜色与 $l_i$ 距离都小于等于 $X$，进而意味着该答案可行。

​ 如何查询所有颜色都出现在了当前区间中？

​ 区间数颜色：对于每个点，记录和它同颜色的点中在它前面离它最近的点（不妨称为它的前驱）的位置，如果该点是该颜色的第一个点，把前驱设为 $-1$ 。特别地，我们在最后面新加一排 $K$ 个点，每个点顺次对应一种颜色，且把它的前驱设为该颜色出现的最后位置。（参照下图理解：我们用箭头表示前驱，最后三个格子是新加的三个点）

​ 我们把所有点的前驱位置放到线段树上。

​ 现设当前我们想知道区间 $[l,r]$ 中是否出现了所有颜色。我们查询区间 $[r+1,n+K]$的最小值，如果该最小值大于等于 $l$ ，则该区间出现了所有颜色。这样做的正确性是显然（？）的：最小值大于 $l$ 意味着所有后面的点的前驱都在 $l$ 之后，而刚刚新加的一排点保证了所有颜色都在 $r$ 后面出现了，于是在 $[l,r]$ 中间必定出现了所有颜色；反之，若最小值小于 $l$，则必定会出现这种情况：

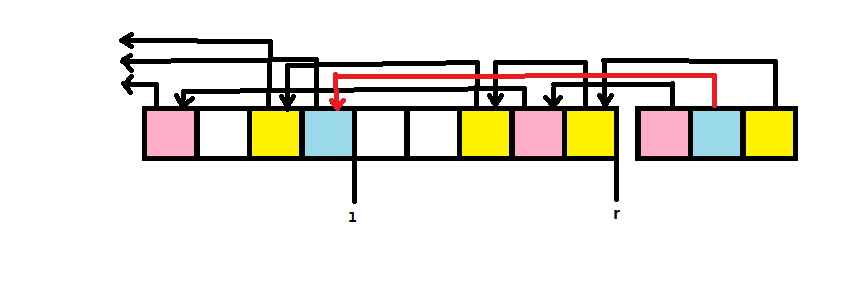
​ 发现，蓝色的前驱“跨过了”该区间，于是蓝色未出现在其中。

​ 线段树区间查询最小值即可。

​ 回到原问题，发现套上二分答案后，我们可以 $O(log^2n)$ 一次询问。考虑加入/删除点的过程，我们可以轻松地使用 set 维护（每种颜色开一个 set，查询前驱后继）然后线段树两次单点修改。于是我们得到一个 $O(Q\log^2n+n \log n)$ 的做法。

​ 考虑优化。刚刚是二分答案+线段树，我们变成线段树上二分：每次二分的答案的右端点为线段树上区间的中点。这样可以把询问降一个 log ，于是用 $O(Q\log n+n \log n)$ 的复杂度通过了本题......吗？

​ 原问题 $x_i$ 的范围很大。我们使用离散化，注意离散化后不要去重。保存离散化后两相邻点的距离。注意一点点细节：新加的一排点位置为 $+inf$ ，每种颜色的第一个点前驱 $-inf$ ，线段树二分的时候算真实距离而不是离散化后的位置之差，把 set 换成 multiset 并且每次只删一个。

​ 据说我码风奇异：

#include<bits/stdc++.h>
#include<algorithm>
#include<set>
#define mid (l+r)/2
#define inf 999999999
using namespace std;
int n,K,Q,m,pb;
int dic[1000001],pdic,stdans[1000001],nu[1000001],ncl;
int seg[4000001],aans[1000001];
multiset<int> se[300001];
struct eve{
	int x,k,l,r;
}a[300001];
struct que{
	int x,t,bh;
}q0[300001];
struct thi{
	int ty,nx,t;
	const bool operator <(thi y)const{if(this->t==y.t)return this->ty<y.ty;return this->t<y.t;}
}b[1000001];
int qread(){int nans=0;char c=getchar();while(c<'0'||c>'9')c=getchar();while(c>='0'&&c<='9')nans=nans*10+c-'0',c=getchar();return nans;}
void putin(){
	n=qread(),K=qread(),Q=qread();
	for(int i=1;i<=n;i++)a[i].x=qread(),a[i].k=qread(),a[i].l=qread(),a[i].r=qread();
	for(int i=1;i<=Q;i++)q0[i].x=qread(),q0[i].t=qread(),q0[i].bh=i;
}
void caldic(){
	for(int i=1;i<=n;i++)dic[++pdic]=a[i].x,b[++pb]=(thi){1,i,a[i].l},b[++pb]=(thi){1,i,a[i].r+1};
	for(int i=1;i<=Q;i++)dic[++pdic]=q0[i].x,b[++pb]=(thi){2,i,q0[i].t};
	sort(dic+1,dic+pdic+1);
	m=pdic+K;sort(b+1,b+pb+1);
	for(int i=1;i<=n;i++){
		int np=lower_bound(dic+1,dic+pdic+1,a[i].x)-dic;
		a[i].x=np+(nu[np]++);
	}
	for(int i=1;i<=Q;i++){
		int np=lower_bound(dic+1,dic+pdic+1,q0[i].x)-dic;
		q0[i].x=np+(nu[np]++);
	}
}
void segbuild(int u,int l,int r){
	if(l==r){
		if(l>pdic)seg[u]=-1;
		else seg[u]=inf;
	}else{
		segbuild(u<<1,l,mid);
		segbuild(u<<1|1,mid+1,r);
		seg[u]=min(seg[u<<1],seg[u<<1|1]);
	}
}
void segadd(int u,int l,int r,int np,int nx){
	if(l==r)seg[u]=nx;
	else{
		if(np<=mid)segadd(u<<1,l,mid,np,nx);
		else segadd(u<<1|1,mid+1,r,np,nx);
		seg[u]=min(seg[u<<1],seg[u<<1|1]);
	}
}
int segreq(int u,int l,int r,int nl,int nr){
	if(l>nr||r<nl)return inf;
	else if(l>=nl&&r<=nr)return seg[u];
	else return min(segreq(u<<1,l,mid,nl,nr),segreq(u<<1|1,mid+1,r,nl,nr));
}
int segef(int u,int l,int r,int nx,int nm){
	if(l==r)return max(dic[l]-nx,nx-dic[nm]);int ng=min(nm,seg[u<<1|1]);
	if(ng!=-1&&(ng==inf||dic[ng]>=max(0,nx-(dic[mid+1]-1-nx))))return segef(u<<1,l,mid,nx,ng);
	else return segef(u<<1|1,mid+1,r,nx,nm);
}
signed main(){
	putin();
	caldic();
	segbuild(1,1,m);
	for(int i=1;i<=K;i++)se[i].insert(pdic+i),dic[pdic+i]=inf;
	for(int i=1;i<=pb;i++){
		if(b[i].ty==1){
			int ni=b[i].nx;
			if(b[i].t>a[ni].r)se[a[ni].k].erase(se[a[ni].k].find(a[ni].x));
			multiset<int>::iterator ii=se[a[ni].k].lower_bound(a[ni].x);
			int np,nq;
			np=*ii;
			if(ii!=se[a[ni].k].begin())nq=*(--ii);else nq=-1;
			if(b[i].t>a[ni].r)segadd(1,1,m,np,nq),segadd(1,1,m,a[ni].x,inf);
			else segadd(1,1,m,np,a[ni].x),segadd(1,1,m,a[ni].x,nq),se[a[ni].k].insert(a[ni].x);
		}else{
			if(segreq(1,1,m,pdic+1,m)==-1)aans[q0[b[i].nx].bh]=-1;
			else{
				aans[q0[b[i].nx].bh]=segef(1,1,m,dic[q0[b[i].nx].x],inf);
			}
		}
	}
	for(int i=1;i<=Q;i++)printf("%d\n",aans[i]);
	return 0;
}

​